Ultra short terahertz pulses excite two-quantum oscillations of atoms in a semiconductor crystal. The terahertz waves radiated by the moving atoms are analyzed by a new time-resolved technique and show the non-classical character of the large amplitude atomic motions.

The classic pendulum of a grandfather clock oscillates back and forth at any time with a well-defined deflection and speed. During this oscillation, its total energy remains constant, which is predetermined by an arbitrarily selectable initial deflection. Oscillators in the quantum world of atoms and molecules behave quite differently: their energy has discrete values corresponding to the different quantum states of an oscillator. The "smeared" location of an atom in an energy eigenstate of the oscillator is described by means of the wave function whose amplitude has no oscillations.

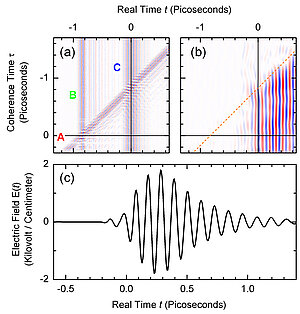
Fig. 1 Experimentally measured curves: (a) Two-dimensional (2D) scan of the sum of the electric fields E(τ, t) of the three driving THz pulses A, B and C as a function of the coherence time τ and the real time t. The contour diagram is colored red for positive electric fields and blue for negative electric fields. (b) 2D scan of the non-linear radiated electric field E_NL(τ, t) from the two-phonon coherence in the semiconductor indium antimonide. The orange line shows the center of THz pulse A. (c) Electrical field transient E_NL(0, t) measured for coherence time τ = 0.

Vibrational motion in the quantum world requires a superposition of different quantum states - so-called coherences or wave packets. The superposition of two adjacent oscillator states corresponds to a one-quantum coherence, in which the atomic motion is very similar to the classical pendulum. Much more interesting are two-quantum coherences, a true non-classical excitation in which an atom can be in two different places at the same time. Its speed also behaves non-classical, which means that it moves from left to right and from right to left at the same time (see Movie). Such movements exist only for very short times, because the well-defined superposition of the quantum states due to the so-called decoherence within a few picoseconds (1 picosecond = 10^-12s) decays. Such two-phonon coherences are extremely important in the new research field of so-called quantum phononics. There, non-classical atomic movements such as "pinched" or "entangled" phonons are studied.

Movie: Illustration of non-classical quantum coherences in matter. The two parabolas (sharp curves) show the potential surfaces of harmonic oscillators, which represent the vibrations of atoms in a crystal around their equilibrium position - the so-called phonons. The blue curves show the residence probability of the atoms at different locations in thermal equilibrium. The quantum-mechanical uncertainty relations force a finite spatial extension of such distribution functions. The red curves show the time-dependent probability of different coherently vibrating quantum states in matter. On the left you can see a one-phonon coherence, in which the quantum-mechanical motion of the atoms is very similar to the classical motion of a pendulum (turquoise sphere). This moves during oscillation either from left to right or from right to left. On the right, we see the time-dependent probability of two-phonon coherence. Quantum mechanics allows a non-classical movement in which an atom can simultaneously stay in two different places. The velocity of the atoms also behaves non-classical, that is, it can swing from left to right and from right to left at the same time. With a perfect harmonic oscillator, the particle currents of these two parts would be extinguished exactly. Therefore, there must be a small anharmonicity so that one can observe the emission of a coherent electric field as in Figure 1 (c).

In the latest issue of the journal Physical Review Letters, researchers at the Max Born Institute in Berlin have used the new method of two-dimensional (2D) terahertz spectroscopy to generate and detect non-classical two-phonon coherences with large spatial amplitudes , In the experiments, a sequence of three phase-locked THz pulses interacts with a 70-μm-thick crystal of the semiconductor indium antimonide (InSb). The electric field emitted by the moving atoms serves as a probe for the atomic movement in real time. A two-dimensional scanning method (a so-called 2D scan), in which the time delay between the three THz pulses is varied, showed pronounced two-phonon signals and was able to reveal their time structure [Fig. 1]. A detailed theoretical analysis has revealed that nonlinear multiple interactions of all three THz pulses are needed to induce such strong two-phonon coherences.

The new experimental method allowed for the first time to detect two-phonon coherences of large amplitude in a crystal. All experimental observations are in excellent agreement with quantum theory. This new type of 2D THz spectroscopy points the way to the generation, analysis, and manipulation of other low-energy excitations in solids, such as, for example. Magnons or optical transitions in excitons or bound to impurities electrons.

Search publications of MBI

Search results

Publications since 2025

Sort: Year Author Title Journal

A1-P-2025.01

Melting, bubblelike expansion, and explosion of superheated plasmonic nanoparticles

S. Dold, T. Reichenbach, A. Colombo, J. Jordan, I. Barke, P. Behrens, N. Bernhardt, J. Correa, S. Düsterer, B. Erk, T. Fennel, L. Hecht, A. Heilrath, R. Irsig, N. Iwe, P. Kolb, B. Kruse, B. Langbehn, B. Manschwetus, P. Marienhagen, F. Martinez, K.-H. Meiwes-Broer, K. Oldenburg, C. Passow, C. Peltz, M. Sauppe, F. Seel, R. M. P. Tanyag, R. Treusch, A. Ulmer, S. Walz, M. Moseler, T. Möller, D. Rupp, B. v. Issendorff

Physical review letters 134 (2025) 136101/1-7

The quantum swing - a pendulum that swings back and forth at the same time

Search publications of MBI

Publications since 2025