The flow of matter, from macroscopic water currents to the microscopic flow of electric charge, underpins much of the infrastructure of modern times. In the search for breakthroughs in energy efficiency, data storage capacity, and processing speed, scientists search for ways in which to control the flow of quantum aspects of matter such as the “spin” of an electron – its magnetic moment – or its “valley state”, a novel quantum aspect of matter found in many two dimensional materials. A team of researchers at the Max Born Institute in Berlin have recently discovered a route to induce and control the flow of spin and valley currents at ultrafast times with specially designed laser pulses, offering a new perspective on the ongoing search for the next generation of information technologies.
Ultrafast laser control over the fundamental quantum degrees of freedom of matter represents the outstanding foundational challenge to be met in establishing future information technologies beyond the semi-conductor electronics that defines our present time. Two of the most promising quantum degrees of freedom in this respect are the spin of the electron and the “valley index”, the latter an emergent degree of freedom of two dimensional materials related to the quasiparticle momentum. Both spintronics and valleytronics offer many potential advantages over classical electronics in terms of data manipulation velocity and energy efficiency. However, while spin excitations suffer from a dynamical loss of character arising from the spin-orbit induced spin precession, the valley wavefunction represents a “data bit” whose stability is threatened only by intervalley scattering, a feature controllable be sample quality. Valleytronics thus presents a potentially robust platform for going beyond classical electronics.
At the heart of any future valleytronics or spintronics technologies will, in addition to quantum excitations encoding data bits, reside the control and creation of valley- and spin-currents. However, while sustained attention has been paid to the task of tailoring lightforms on ultrafast time scales to selectively excite valley quasiparticles, the precise creation and control of valley-currents and spin-currents – vital for any future valleytronics technology – has remained beyond the realm of ultrafast light control. In a study recently published in Science Advances, a team of researchers from the Max Born Institute in Berlin have shown how a hybrid laser pulse combining two polarization types allows complete control over ultrafast laser-light-induced currents.
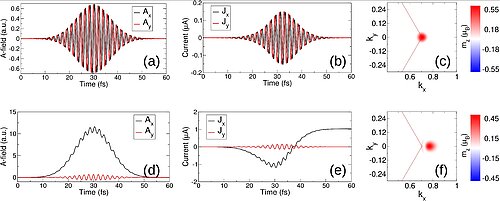
Control over the charge state by circularly polarized light is now well established, the famous “spin-valley locking” of the transition metal dichalcogenides that has its origin in the valley selective response to circularly polarized light. This can be viewed as arising from a selection rule involving the magnetic quantum numbers of the d-orbitals that comprise the gap edge states. While circularly polarized light excites valley charge it does not, however, create a valley current as shown in Fig. 1a,b. This situation arises as for each quasi-momentum in the valley kvalley that is excited a corresponding −kvalley, also is excited: the Bloch velocities thus cancel and there is no net valley current.
Full control over light induced valley currents, their magnitude and direction, thus requires going beyond the spin-valley locking paradigm of circularly polarized light. Creation of a valley excited state that does result in a net valley and spin current must therefore involving breaking the local kvalley, −kvalley degeneracy. As the laser vector potential couples directly to crystal quasi-momentum, k → k − A(t)/c, the most effective way in which this can be done is through a linearly polarized single cycle pulse with duration comparable to that of the circularly polarized pulse: such a pulse will evidently be in the "THz window" of 1 THz to 50 THz. As shown in Fig. 1d,e the hencomb lightform generates a substantial residual (i.e. persisting after the laser pulse) current. This results from a non-cancellation of the Bloch velocities of excited quasi-momentum, as the distribution of excited charge is now shifted off the high symmetry K point by exactly the polarization vector of the THz pulse, as shown in Fig. 1f.
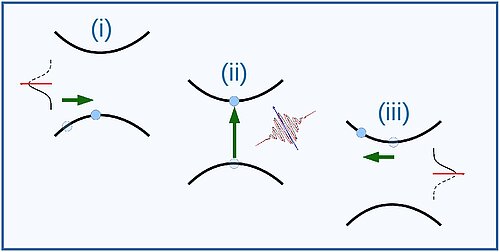
The physical picture underpinning the action of this pulse is schematically illustrated in Fig. 2: a half cycle of the THz component of the hencomb pulse drives an intraband motion sending states distant from the gap edge to the gap edge (i). At this point the circularly polarized component excites this charge across the gap (ii), with finally the second half cycle of the THz component returning the charge to its original momentum (iii). In this way charge has been excited at a quasi-momentum q with conduction-valence energy difference, ϵc − ϵv, that is not equal to the circularly polarized light energy ℏωcirc (and hence not equal to the band gap to which this light is tuned). The polarization vector of the THz light component represents the key control parameters of a hencomb pulses, with the polarization direction and amplitude respectively determining the direction and amplitude of the light induced current. In the way such hencomb pulses represent a route to the direct light control over simultaneously the charge and current state of valley active two dimensional materials, offer a new route towards valleytronics and spintronics at ultrafast times.