Diese nicht eingängigen Aussagen der Quantenmechanik beruhen auf der Tatsache, dass jede Messung an einem quantenmechanischen System nur ein Ergebnis aus einer großen Menge von möglichen Resultaten hervorbringt. Die Wahrscheinlichkeit, ein bestimmtes Ergebnis zu erhalten, wird durch eine Wahrscheinlichkeitsverteilung beschrieben, die aus der Wellenfunktion - einem fundamentalen Objekt der Quantenmechanik - abgeleitet wird. Die Wellenfunktion selbst ist nicht direkt messbar. Man kann jedoch Strategien entwickeln, wonach durch mehrfache Messung an einem quantenmechanischen System die Wellenfunktion komplett charakterisiert werden kann.
In einer Arbeit (Villeneuve et al., "Coherent Imaging of an Attosecond Electron Wave Packet"), die in Science veröffentlicht wurde, wird ein neuer Ansatz für die vollständige Charakterisierung einer atomaren Wellenfunktion mit Hilfe von neuartigen ultraschnellen Lasern, die erst vor wenigen Jahren entwickelt wurden, präsentiert. In den Messungen charakterisieren die Wissenschaftler die Wellenfunktion eines Elektrons, das nach der Wechselwirkung von einem Neon-Atom mit einer Serie von Laserpulsen erzeugt wird.
Ein perfektes Attosekunden-Experiment
Die Entwicklung der Quantenmechanik in den ersten Jahrzehnten des vorigen Jahrhunderts zwang Wissenschaftler dazu zu akzeptieren, dass sich Materie auf der mikroskopischen Skala nach physikalischen Regeln verhält, die sich grundsätzlich von den in der makroskopischen Welt unterscheiden. In der mikroskopischen Welt spielen Konzepte wie die Unschärferelation eine Rolle, die die Genauigkeit beschreibt, mit der man bestimmte Eigenschaften kleiner Teilchen, z.B. ihren Ort und ihre Geschwindigkeit, zeitgleich messen kann. Darüber hinaus führt die Quantenmechanik den Welle-Teilchen-Dualismus ein, der besagt, dass das Verhalten von kleinen Teilchen manchmal besser durch Welleneigenschaften verstanden werden kann.
Elektronen sind Elementarteilchen, die für so alltägliche Dinge wie die Elektrizität verantwortlich sind. Sie werden z.B. durch ihre (negative) Einheitsladung charakterisiert. Daneben haben sie auch einen Drehimpuls. Das ist ein Vektor, der die Rotation des Elektrons um das Zentrum eines Atoms beschreibt. Eine langsame Rotation oder eine Rotation in der Nähe des positiv geladenen Atomkerns entspricht einem niedrigen Drehimpuls, während eine schnelle Rotation oder eine Rotation weit entfernt vom Kern zu einem hohen Drehimpuls führt. Die Regeln der Quantenmechanik legen fest, dass der Drehimpuls nur bestimmte Werte annehmen kann. Folglich werden Drehimpulszustände mit "s", "p", "d" und "f" bezeichnet, was den Drehimpulsquantenzahlen l=0-3 entspricht. Neben der Größe des Drehimpulses spielt die Projektion des Drehimpulsvektors auf eine gewählte Achse im Laborsystem (z.B. die Polarisationsachse des im Experiment benutzten Lasers) - charakterisiert durch die magnetische Quantenzahl m - für das Ergebnis und die Interpretation von Laborexperimenten eine Rolle.
In der Veröffentlichung beschreiben die Wissenschaftler wie es Ihnen gelungen ist, die Wellenfunktionen eines ionisierten Elektrons, das Beiträge des Drehimpulses bis zu einem Wert l=3 (d.h. s, p, d, und f-Beiträge) enthält, vollständig zu charakterisieren. Jeder dieser Drehimpulszustände ist in der Wellenfunktion mit einer bestimmten Amplitude und Phase enthalten. Diese Amplituden und Phasen werden nun durch eine Serie von Interferenzexperimenten bestimmt. Hierbei wird die Wellennatur des quantenmechanischen Teilchens ausgenutzt. Genau wie bei zwei sich kreuzenden Wasserwellen, die sich entweder verstärken oder auslöschen, können auch Interferenzen zwischen verschiedenen Teilen einer quantenmechanischen Wellenfunktion zu einer Erhöhung oder Reduktion der Wahrscheinlichkeit führen, mit der ein Teilchen an einem bestimmten Ort oder mit einer bestimmten Geschwindigkeit nachgewiesen wird. Indem nun eine Reihe von Interferenzexperimenten mit unterschiedlichen Bedingungen durchgeführt wird, kann die paarweise Interferenz zwischen dem s- und d-Anteil der Wellenfunktion, dem p- und f-Anteil und schließlich zwischen allen vier Komponenten beobachtet werden (siehe Abbildung 1). Demensprechend wurde ein präziser und vollständiger mathematischer Ausdruck für die Wellenfunktion des ionisierten Elektrons erhalten.
Eine entscheidende Komponente für den Erfolg dieser einzigartigen Leistung war der Einsatz von Attosekunden-Laserpulsen (1 as = 10-18 s). Attosekundenpulse sind die kürzesten Laserpulse, die in modernsten Laserlaboratorien erzeugt werden können. Sie werden in einem Prozess erzeugt, der "Erzeugung hoher Harmonischer" (engl. high-harmonic generation) genannt wird. Hierzu wird ein atomares Edelgas einem intensiven Infrarot(IR)-Laserpuls ausgesetzt, der typischerweise eine Dauer von wenigen Femtosekunden (1 fs = 10-15 s) hat. Wenn die Intensität des Infrarot-Lasers hoch genug ist, kann das Laserfeld Elektronen aus dem Atom herausziehen, die anschließend im oszillierenden elektrischen Feld des Infrarot-Lasers beschleunigt werden. Einige der beschleunigten Elektronen stoßen dann mit dem Atom zusammen, aus dem sie entfernt wurden. In diesem Fall kann das Elektron von dem Atom wieder aufgenommen werden. Die gesamte Energie, die für die Ionisation und Beschleunigung des Elektrons aufgebracht wurde, wird dann in der Form eines hochenergetischen Lichtpartikels (d.h. eines Photons im extremen ultra-violetten (XUV) oder weichen Röntgen-Bereich des elektromagnetischen Spektrums) freigesetzt. Da die verschiedenen Schritte der Erzeugung hoher Harmonischer auf einer Zeitskala ablaufen, die kurz im Vergleich zur Dauer einer optischen Schwingung des Infrarot-Lasers (typischerweise wenige Femtosekunden) ist, erscheint dieses XUV/Röntgen-Licht in der Form eines kurzen Attosekunden-Pulses.
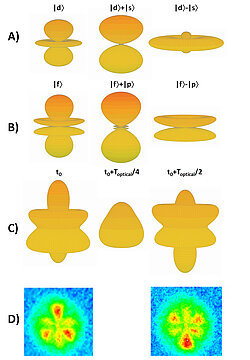
Abbildung 1: A) Die Ionisation mit dem XUV-Pulse alleine erzeugt ein Elektron in einem Zustand, der durch "s"- und "d"-Drehimpulse charakterisiert wird. Durch eine Messung der Elektronenwinkelverteilung wird die relative Amplitude und Phase zwischen beiden Komponenten bestimmt; B) XUV+IR-Ionisation erzeugt ein Elektron in einem "p"- und "f"-Drehimpulszustand. Wieder wird die relative Amplitude und Phase aus der Messung der Elektronenwinkelverteilung bestimmt; C) Die kombinierte XUV-alleine- und XUV+IR-Ionisation erzeugt Elektronenwellenfunktionen, die sowohl "s", "p", "d" und "f" Beiträge enthalten. Die Interferenzen zwischen diesen Drehimpulskomponenten ändern sich mit der Verzögerung zwischen XUV-Puls und ko-propagierendem IR-Puls. Der große Beitrag der "f"-Komponente ist deutlich im ersten und letzten Bild sichtbar; D) Gemessenes Elektronenimpuls-Bild bei zwei Zeitverzögerungen zwischen XUV-Puls und IR-Puls (entsprechend dem ersten und letzten Bild in C). Das vorliegende Experiment ermöglicht eine komplette Bestimmung der relativen Amplitude und Phase aller Drehimpulskomponenten und repräsentiert daher ein "perfektes" Experiment.
In dem Experiment haben die Forscher Attosekunden-XUV-Pulse dazu benutzt, Neonatome zu ionisieren. Wenn im Experiment nur der Attosekundenpuls gefeuert wird, wird eine Kombination von s- und p-Elektronen erzeugt, deren Amplitude und relative Phase aus der gemessenen Winkelverteilung bestimmt werden kann (siehe Abbildung 1A). Wird neben dem Attosekundenpuls zusätzlich eine Kopie des Infrarot-Laserpulses zur Ionisation benutzt, können die Amplitude und relative Phase der p- und f-Komponenten gewonnen werden (siehe Abbildung 1B). Werden schließlich die Attosekundenpulse mit Hilfe eines Zwei-Farben-Laserfelds (d.h. sowohl mit dem erwähnten Infrarot-Laserpuls als auch mit einer Kopie dieses Pulses bei halber Wellenlänge) erzeugt und zusammen mit dem Infrarot-Puls benutzt, kann bei der Ionisation die Amplitude und relative Phase von allen vier Komponenten (s, p, d und f) bestimmt werden. Das Ergebnis des Experiments und die ermittelten Amplituden und Phasen aller Drehimpulskomponenten sind in Abbildung 1C und 1D dargestellt. Die deutlich sichtbare sechsfache Struktur wird durch den dominanten Beitrag des f-Orbital mit m=0 bei der XUV+IR-Ionisation hervorgerufen. Durch die kohärente Überlagerung eines Beitrags des vollständig symmetrischen s-Orbitals (erzeugt nur durch den XUV-Puls) und die Änderung der Verzögerung zwischen XUV- und IR-Puls kann eine Auf- und Aboszillation entlang der vertikalen Laserpolarisation erzeugt werden, die die Phase des f-Orbitals sichtbar macht.
Dieses Experiment ist, was Atomphysiker als ein "komplettes" Experiment erachten, da es eine vollständige mathematische Beschreibung der Wellenfunktion des ionisierten Elektrons ermöglicht. Es ist darüber hinaus das neueste Beispiel dafür, wie die Attosekundentechnologie derzeit die ultraschnelle Laserphysik revolutioniert. Mit der vorliegenden Arbeit hat diese Forschung zum ersten Mal einen Zustand der Perfektion erreicht. (Textübersetzung: Dr. Claus-Peter Schulz)